Smooth to the Touch
29 May 2020Dr Mark Irle of Ecole Supérieure Du Bois and Prof Lidia Gurau of the University of Transylvania explain their research into measuring the surface roughness of wood-based panels
More than half of all particleboard and MDF panels have some kind of finish applied to their surfaces. Whether this finish is a paper laminate, PVC foil, paint or something else, all require smooth, uniformly light-coloured surfaces. Good quality surfaces ease the application of the finishes and reduce finishing costs.
Consequently, panel surface quality can have a major impact on the overall production cost of a final product.
The process step that differentiates wood-based panels (WBP) from other wood products is the hot-pressing step, which for particleboard and MDF, involves very high pressures. When panels exit the hot-press they “springback” a little and because wood is a naturally variable material the amount of springback varies within and between panels. Accordingly, WBP are not just sanded for surface quality but also to ensure reliable thickness calibration.
All WBP production lines need to follow how panel surface quality changes as the sanding belts wear. In the vast majority of cases, companies rely on the experience of operators to adjust sanding settings and fixed protocols on when to change the belts.
There are two aspects to optimising the sanding process: (a) the appropriate selection of sanding parameters (belt type, grit size, sanding pressure, running speed, among others; and (b) the best time to change the belts. Both of these optimisation steps could be assisted by the continuous measurement of surface quality and, in this article, we are focusing on surface roughness.
Our eyes and fingers are quite good at sensing the “undulations” of a surface, ie its texture, in a qualitative way, but, not quantitatively. Quantitative measurements can be acquired by a multitude of methods; the most common of which are:
- Light scattering of an inclined, collimated light beam
- Stylus
- Laser triangulation
Method 1 uses a correlation between the roughness of a surface and the amount of light it scatters; as rough surfaces tend to scatter light more than smooth ones. The correlation has to be performed on the target material because different materials scatter light in different ways.
The GreCon SUPERSCAN surface analyser uses a version of this technology. The inclined beam method is not able to achieve the same precision as the other two methods, but it has sufficient accuracy for surface roughness evaluation in an industrial environment and it is able to scan the whole panel surface at commercial line speeds.
Figure 1 shows a typical stylus used for surfaces like wood. The vertical resolution (z direction) can be in the nanometre range. The horizontal resolution (x-direction) along the trace can be chosen by the user and for wood surfaces we recommend 5μm.
Multiple parallel scans can be performed so as to obtain an area profile. The distance between the scans determines the y-direction resolution. Scanning areas can take a long time and so, frequently, single traces are used to characterise a surface. The advantage of method three over the stylus method is that it is a non-contact method and can scan quickly. The operating principle is laser triangulation where the angle of a reflected laser beam is dependent on the distance the beam has travelled, so it can discriminate between different surface heights. The outputs are the same as those for the stylus and the profiles are processed in exactly the same way.
Methods two and three generate traces of a surface’s topography; an example is shown in Figure 2. The profile consists of an “x” value that represents the distance that the stylus or laser has moved and a “z” value that shows the height of the surface at that point (somewhat confusingly, the z value is shown on what is conventionally the y-axes of the graphs overleaf). Most profiles include some form errors, like that in Figure 1, and waviness errors that are caused by things like machine vibrations. These must be removed mathematically to reveal the roughness of the surface itself.
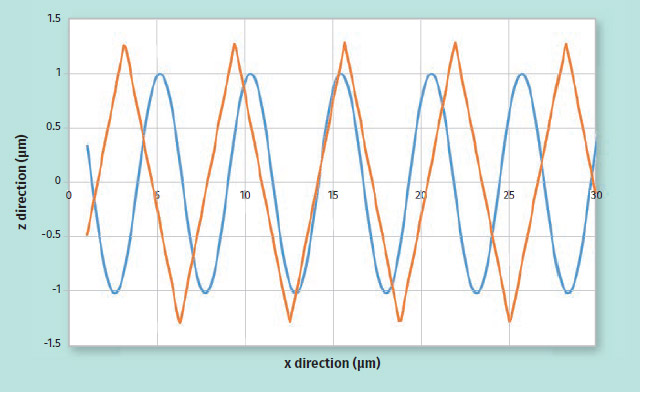
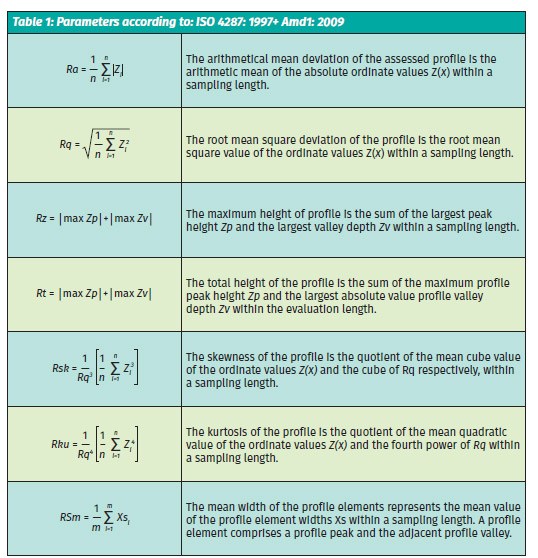
Methods two and three generate roughness profiles that can be analysed to calculate a wide range of roughness parameters. Roughness parameters facilitate comparisons between surfaces prepared using different processing set-ups. Although the range of parameters suggested by standards like ISO 4287: 1997+ Amd1: 2009 are quite comprehensive, only a few are used in practice. The most commonly used parameter is Ra, which is the arithmetic mean of the absolute values for the heights of the peaks and the depths of the valleys, ie the z values, which are converted to positive numbers and then averaged. A perfectly smooth surface (which does not exist) has a Ra value of 0; the bigger the Ra the rougher the surface. The reason why Ra alone is not enough is shown in Figure 3, which shows two surface profiles with the same Ra value.
The zigzag line has higher peaks, deeper valleys and sharp transitions compared to sinusoid curve, so clearly, they would feel different to the touch.
The definitions of a number of roughness parameters are given in the calculation tables. We recognise that many readers will be put off by the mathematics involved and so here we do not go into too many details but describe why each might be useful. Ra and Rq are not sensitive to isolated extreme irregularities whereas the height parameters Rt, Rz and shape parameters Rsk and Rku are. Rt and Rz quantify the highest amplitude of irregularities, which can help distinguish between various surfaces.
Surfaces that have fairly deep valleys in a smooth plateau, like finely sanded oak, will have a negative Rsk parameter.
Rku measures kurtosis, so it is influenced by isolated peaks or valleys and so it can identify the presence of fairly deep valleys or high peaks in a profile.
RSm is a measure of the width of irregularities. The larger these irregularities are, the higher is the RSm. This parameter is useful because it indicates the size of gaps in the surface.
Rpk, Rk and Rvk from ISO 13565-2: 1996 + Cor 1:1998 can be used to describe the roughness of the machining process itself. Rk characterises the core of the roughness profile. This parameter will be influenced by the processing variables, for example, grit size, but can also vary with the composition of the panels themselves, for example, the species, and the size of particles.
This article may have shown you that measuring surface roughness is rather more complicated than you thought. We have only given what we think are the most relevant aspects to the WBP industry. We are willing to try to answer your questions because proper surface roughness analysis can give very useful information to a production engineer.
 Figure 1. A weathered piece of oak that is about to be scanned by a stylus type surface roughness analyser (photo by Julia Buchner, PhD researcher at ESB). The piece is clearly cupped and so this form error must be removed before calculating the surface roughness parameters
Figure 1. A weathered piece of oak that is about to be scanned by a stylus type surface roughness analyser (photo by Julia Buchner, PhD researcher at ESB). The piece is clearly cupped and so this form error must be removed before calculating the surface roughness parameters
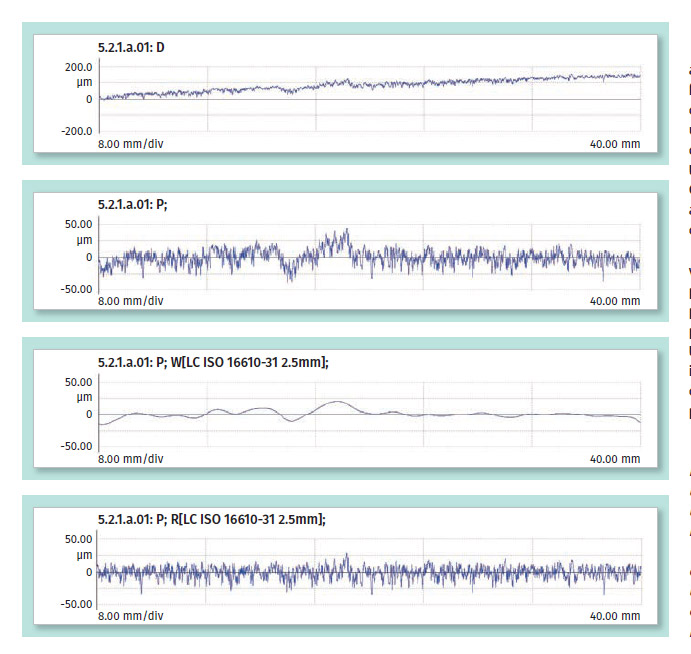 Figure 2. A profile of an MDF surface. The top trace is the recoded profile. The second is the same profile but with the form error (slope) removed and is termed the Primary profile. The third image shows the waviness profile contained in the Primary profile. The final trace contains only the surface roughness data and this can be used to calculate the surface roughness parameters
Figure 2. A profile of an MDF surface. The top trace is the recoded profile. The second is the same profile but with the form error (slope) removed and is termed the Primary profile. The third image shows the waviness profile contained in the Primary profile. The final trace contains only the surface roughness data and this can be used to calculate the surface roughness parameters